CSAPP3e第二章(整数的表示)

发表于 2025-01-19 更新于 2025-02-21 分类于组成原理阅读次数：

整数的表示(第二章 Part1)

~~博客还没装 Mathjax 插件，所以下面的 $\LaTeX$ 应该都是乱的~~ 已修

整数表示

这一段如果没有目的和顺序地硬看会觉得关系很多很复杂，但其实只要按照一定的目的和顺序结构就会很清晰。

以设计者的视角思考如何设计

如果我们是设计用二进制表示整数的人，我们需要如何表示二进制？

利用 $w$ 位二进制的最高位 $ x_{w-1} $ 为 $1$ 代表这个数是负数，剩下的部分正常用二进制表示即 $\displaystyle\sum_{i=0}^{w-2}x_i\cdot2^i$

但显然光表示是完全不够的，我们还需要运算，而符号位由于不对具体数值做贡献，会导致运算错误。 因此我们需要让符号位也代表数值，用另一种映射方式计算，于是我们令最高位的符号位具有负的权重 $-x_{w-1} \cdot 2^{w-1}$，这样符号位也参与了计算。但是这样数值又对不上了，因此我们需要把后面的位也变一下。由于我们不是真的设计师，所以我们直接看答案：取反后面的每一位后再 +1。例如10010除符号位取反后变为11101， +1后是11110。这样的表示方法计算出的数值是 $-x_{w-1}\cdot2^{w-1}+\displaystyle\sum_{i=0}^{w-2}x_i\cdot2^i$ 如何论证这样的数值是对的呢？

我们称10010 11101 11110 这样的二进制形式为位模式或位向量。Formally, $w$ 位的位向量 $\vec{x_w}=[x_{w-1}, x_{w-2}, ..., x_1, x_0]$ (其中 $x \in \{0, 1\}, \text{ where } x \in \mathbb{Z}$)。另外，称一开始的符号位不参与计算的位模式为原码，除符号位取反后的位模式为反码，取反后+1的为补码。我们还将以无符号整数形式(即所有位模式都是 $2^{i}$ 的权值)解释位模式所计算出的十进制数值这个过程写作一个函数 $B2U(\vec{x_w})$ 即 Binary to Unsigned，易得$B2U(\vec{x_w}) = \displaystyle\sum_{i=0}^{w-1}x_i\cdot2^i$。类似地，我们有以反码形式解释位模式所计算出的十进制数值 $B2O(\vec{x_w})$ 和以补码形式解释位模式所计算出的十进制数值 $B2T(\vec{x_w})$。对应地，我们也有这些函数的反函数$U2B(x), T2B(x), O2B(x)$。

则我们需要证明的问题以数学语言描述就是，设 $B2T(\vec{x_w}\prime) = -x_{w-1}\prime\cdot2^{w-1}+\displaystyle\sum_{i=0}^{w-2}x_i\prime\cdot2^i$ 那么我们需要表示的数值 $x = -\displaystyle\sum_{i=0}^{w-2}x_i\cdot2^i = B2T(\vec{x_w}\prime)$, 其中 $\vec{x}\prime$ 是 $T2B(x)$ 即原码 $\vec{x_w}$ 取反后 + 1的位模式。(正数的无符号表示、原码、反码、补码都一样，以下只考虑负数)

考虑到 +1 导致的进位影响我们对 $\vec{x_w}\prime$ 的表达，我们借助反码 $\vec{x_w}\prime\prime$，根据定义得知 $B2O(\vec{x_w}\prime\prime) + 1 = B2T(\vec{x_w}\prime)$ 。则 $x_i\prime\prime = (1 - x_i)$一个连等式就能证明全部：

~~(沟槽的 hexo-filter-mathjax 插件有 Bug，我本地 MarkText 的 Mathjax 正常解析多行，这里就变单行了，对付看罢。)~~ 已修

\[ \begin{aligned} x &= -\displaystyle\sum_{i=0}^{w-2}x_i\cdot2^i \\ &= -2^{w-1} + 2^{w-1} - 1 - \displaystyle\sum_{i=0}^{w-2}x_i\cdot2^i + 1 \\ &= -2^{w-1} + \displaystyle\sum_{i=0}^{w-2}2^i - \displaystyle\sum_{i=0}^{w-2}x_i\cdot2^i + 1 \\ &= -2^{w-1} + \displaystyle\sum_{i=0}^{w-2}(1-x_i)\cdot2^i + 1 \end{aligned} \]

其中 $(1-x_i)$ 即反码的位模式 $x_i\prime\prime$，这样我们证明了补码的数值转换函数$B2T(\vec{x_w}) = -x_{w-1}\cdot2^{w-1}+\displaystyle\sum_{i=0}^{w-2}x_i\cdot2^i$ 的数值表示是正确的(实际上这个函数是一个双射)，而此时符号位也参与了运算，所以这套表示体系也能正常参与运算（后面会更详细地说明运算问题）

事实上，补码也能正常参与运算，只是对 0 的表示有两种 (0000 和 1111) 。

给出补码的数值转换函数 $B2O = -x_{w-1}\cdot(2^{w-1}-1)+\displaystyle\sum_{i=0}^{w-2}x_i\cdot2^i$

如何取负？

既然我们有了补码的定义，很容易就知道对一个数 $x$ 取相反数就是令 $x$ 的补码 $\vec{x_w}$ 所有位 取反然后再 +1。

Q: 为什么是所有位取反？补码不是除符号位取反再 +1 吗？

A: 取相反数符号位肯定要变化啊。我们是+3 -> -3

注意到这个其实就是 $-x = (2^w - x) \mod 2^w$，注意不到也没关系，~~因为我就没注意到~~，后面还会继续说这个事。

想一想，设 $\mathrm{TMin}$ 为 $w$ 位补码表示的最小数值，那么：
$\mathrm{TMin}$ 的补码位模式(即 $T2B(\mathrm{TMin})$ ) 是多少？
  int custom_abs(signed int x) {
      if(x < 0) return -x;
      return x;
  }
这段代码有什么问题？

补码的不对称性

根据上面的问题，我们发现 custom_abs(TMin) 返回的还是 TMin.

在补码语境下，由于符号位是 1 表示的都是正数，符号位是 0 的表示的都是非负数，这两者表示的数字个数相等，而 0 不是正数也不是负数，但它是非负数，所以表示的正数比负数少一个，所以 $\mathrm{TMax + 1 = abs(TMin)}$ , 例如对 4 字节正数，最大值是 $2^{31} - 1 = 2147483647$, 而最小值是 $-2^{31} = -2147483648$。

在 C 和 C++ 语言中，unsigned修饰的无符号数以无符号形式解释，即我们的 $B2U$，其他的则以补码解释。

Java 以补码解释。Rust i32 i64 等以补码表示，u32 等以无符号数形式解释。

C 和 C++ 的 unsigned 溢出是行为良好的，上下溢出都是循环，但有符号正数的溢出是未定义行为。注意浮点数的溢出也是行为良好的，因为 IEEE 754 规定了溢出产生正负无穷。

Java 的溢出是行为良好的，按照补码规则循环环绕到最小值

Rust 的溢出取决于编译模式，Debug 模式会触发panic ，Release 模式类似 Java。

Python 不太清楚具体怎么表示的，理论上只要内存够应该不存在溢出的情况？我还在学 py。

无符号数解释和补码解释的关系

对于一个位模式 $\vec{x_w}$ 以无符号数解释的数值 $B2U(\vec{x_w})$ 和以补码解释的数值 $B2T(\vec{x_w})$ 有什么关系？考虑这两者的公式（设 $x_{w-1} = 1$ )：

$B2U(\vec{x_w}) = \displaystyle\sum_{i=0}^{w-1}x_i\cdot2^i = x_{w-1}\cdot2^{w-1}+\displaystyle\sum_{i=0}^{w-2}x_i\cdot2^i$

$B2T(\vec{x_w}) = -x_{w-1}\cdot2^{w-1}+\displaystyle\sum_{i=0}^{w-2}x_i\cdot2^i$

发现只有最高为的权重正负不同，即两者只差 $2 \times 2^{w-1} = 2^w$

当然如果是正数，$x_{w-1} = 0$ 则二者相等。

故：$B2U(\vec{x_w}) - 2^w = B2T(\vec{x_w})$

于是就有了这个经典的图：

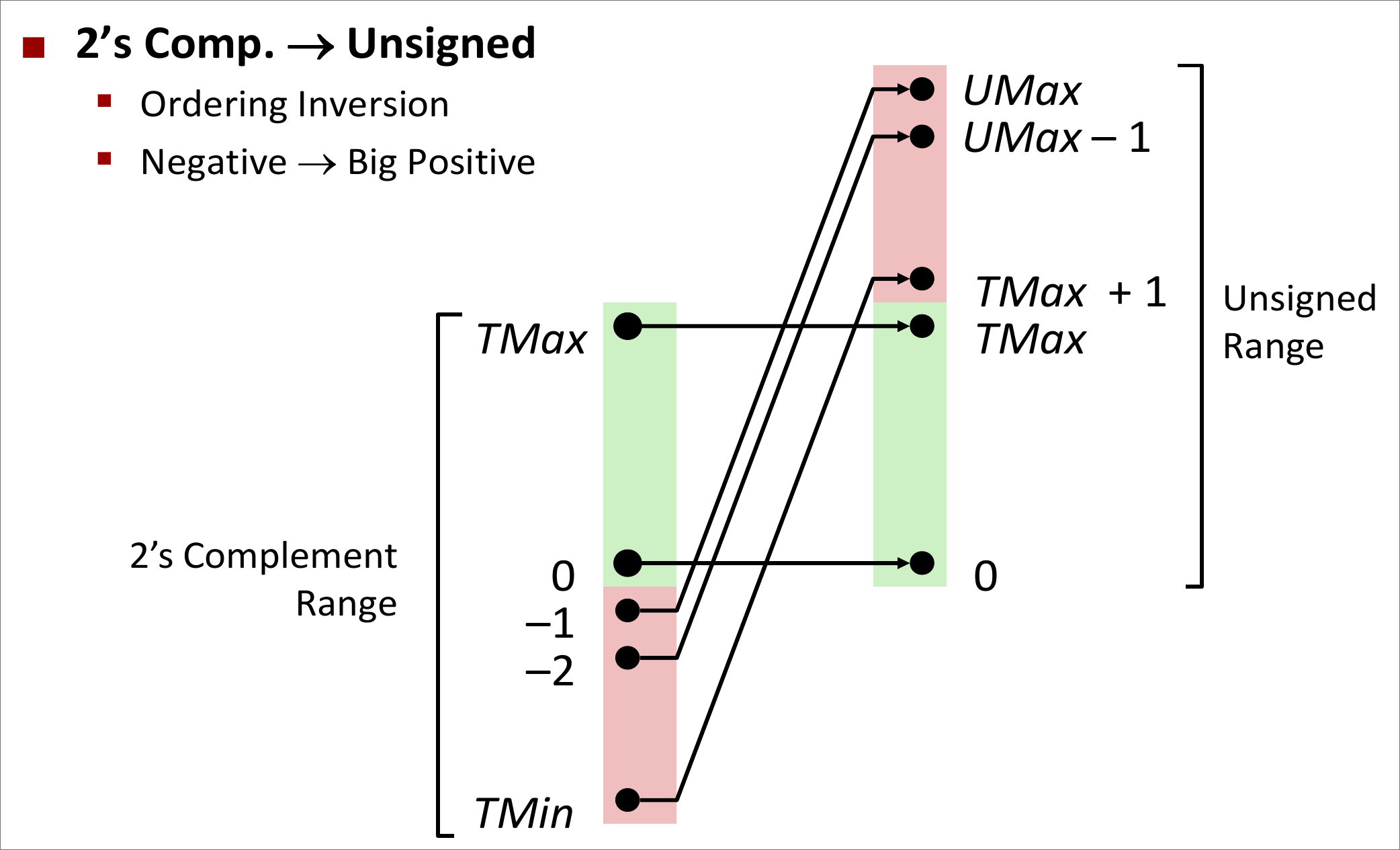
取相反数

我们上面说了取相反数就是 $-x = (2^w - x) \mod 2^w$ .下面来证明一下。

Formaly, 我们需要证明 $U2B(2^w - b) = T2B(-b)$ ,急症 $B2T(U2B(2^w - b)) = -b $

由上面说到的 $B2U(\vec{x_w}) - 2^w = B2T(\vec{x_w})$ ，令 $x = U2B(2^w - b)$

得 $B2T(U2B(2^w - b)) = B2U(U2B(2^w - b)) - 2^2 = 2^w - b - 2^w = -b$

得证。

举个例子:

$T2B(-3) = U2B(2^w - 3) = T2B(-3)$

扩展和截断

无符号数扩展直接补 $0$ 在前面, 补码扩展在前面补 $1$, 可以证明是正确的。

截断无符号数相当于对 $2^k$ 取模, 截断补码相当于位模式下截断无符号数再转换为补码表示。

换句话说就是：无符号数和补码的操作在位级表示上是相同的, 这一点会在后面大量用到。

总结:

这里我们用数学公式以权重的方式解释了补码的表示原理和常用的转换关系。

从不过这部分的知识可以以更优雅的方式即群论表示。

补码实际上就是模 $2^w$ 的同余群。