CSAPP3e第五章(优化程序性能)

发表于 更新于 分类于 阅读次数：

第五章 优化程序性能(摘要与注解)

我错了,我明天一定把这一篇补完

我对了,我今天把这一篇补完了

感觉是本书最难理解和应用的一章, 所以得多花点功夫尽可能深入理解了然后写的好一点

影响优化的细节

有些问题导致编译器不敢放开手脚优化, 所以一味依赖编译器优化是不可行的
常见的影响优化的问题(可能在极端情况下, 优化后的程序与优化前的执行结果不同):

  1. 内存别名使用(两个指针实际指向同一地址, 看似相同的操作也会产生差异)
1
2
3
4
5
6
7
void add1(long *xp, long *yp) {
    *xp += *yp;
    *xp += *yp;
}
void add2(long *xp, long *yp) {
    *xp += 2 * *yp;
}

函数add1需要 2 次读 yp, 两次读 xp, 两次写 xp, 函数add2 需要一次读 yp, 一次读 xp, 一次写 xp,明显后者更优
那么函数add1可能被优化为add2吗? 答案是否定的, 如果 xp 和 yp 指向相同的内存地址, 这两者的行为会不同

  1. 函数调用的副作用(导致编译器不能按照表达式求值相等而优化, 副总用必须被考虑)
1
2
3
4
5
6
7
long f();
long foo() {
    return f() + f() + f() + f();
}
long bar() {
    return 4 * f();
}

foo 有四次函数调用(压栈保存上下文出栈返回), 显然我们觉得bar的效率更优, 但这里同样也是不能优化的, 因为函数的返回值除了被用来 eval expression, 同时也可能有副作用, 比如 f() 里会修改一个全局变量, 成为一个有状态的函数, 这里的行为就不同了。

附加阅读:

  • 纯函数（Pure Function）：函数式编程的核心, 具有引用透明性并且无副作用. 引用透明性是指相同输入一定有相同输出, 无副作用是指不修改外部状态(全局变量, I/O 操作等)
  • 副作用（Side Effect）：修改全局变量、进行 I/O 操作、抛出异常、写日志、改变参数本身等等。
  • 优化: 由于纯函数的输出仅依赖于输入且无副作用，编译器可以安全地进行优化。比如 Haskell 和 Lisp 这种位于鄙视链顶端的顶级函数式语言对纯函数有很严格的要求使得编译器易于优化

表示程序性能

最先想到的肯定是时间复杂度用具体的时间单位(s, ms, ns, ps), 但是不同机器上无法控制变量(比如拿 ENIAC 跑出来的时间和现在 9800x3d 跑出来的结果肯定是不同的, 不然 AMD 不是白设计了吗), 所以考虑掉抽象掉一部分不重要的内容, 于是便有了 CPE 和 时间复杂度两个概念, 后者抽象的程度比前者更深

首先要考虑除以每个时钟周期的时间, 得到时钟周期数, 这样就是机器无关的了, 但是这样的时钟周期数太笼统, 不方便我们具体分析最耗时的瓶颈, 所以引入 CPE 的概念:

CPE (clocks per element, 处理每个元素的时钟周期数), 乘以时钟周期的纳秒数就是每个元素实际处理的时间

与时间复杂度比较 (\(T(6n^3+3n^2\log{n}) = O(n^3), \text{CPE} = 6\)), 时间复杂度要抽象掉的东西更多

读完这一章可以发现这种视角的优化程序是在 \(n\) 不变时通过对程序(或者说超标量的现代CPU)运行的理解来优化程序, 而算法和数据结构是制止 \(n\) 增大时程序运算次数的暴力上涨趋势

实际上由于 CPU 的执行方式(乱序处理投机执行)很难完全用人脑分析, 所以 CPE 大部分时候是测出来然后去想为什么会这样反推原因, 下面会说 CPU 的指令执行方式和具体剖析优化程序的实例.

常见优化方法

  1. 代码移动, 如果有要执行多次但不会改变计算结果的计算, 可以摘出循环, 经典例子如 strlen(s) 是 \(O(n)\) 的而不是 \(O(1)\) 的, 写在循环的判断条件里就变成 \(O(n^2)\) 了, 而且这种地方是现代编译器不敢去优化的地方
1
2
3
4
5
6
7
8
for(size_t i = 0; i < strlen(str); i++) {
    ...
}
// 优化为
size_t len = strlen(str);
for(size_t i = 0; i < len; i++) {
	...   
}

编译器不优化是它不知道你会不会在循环里修改某些状态导致 strlen(str) 的返回值出现变化。
代码移动的一个重要应用场景就是减少过程调用(第三章很简单所以我没写, 根据第三章, 函数调用要压栈保存上下文压返回地址然后跳转到新栈帧, 返回后还得恢复上下文, 还有调用约定, caller-saved callee-saved等等, 所以比较费时间), 把循环中反复出现的返回值固定的无副作用函数调用从放到循环外面。

  1. 消除不必要的内存引用, 栈内存相比寄存器的速度是很慢的, 下一章的博客(其实我第五章是第六章之后写的)有提到就是 DRAM 和 SRAM 的速度差距, 经典例子是 *dest = *dest + data[i] for i; 改为 acc += data[i] for i; *dest = acc;, acc 可以优化到寄存器 (SRAM) 中, 显然比每次都访存要快很多。不过这个其实在某些情况下是改变了原意的, 比如 dest 和 data 指向相同位置(还记得吗? 内存别名使用)
    -O2 的实现方式很巧妙而且不会改变原语义:

    1
    2
    3
    4
    5
    6
    .L22
    	vmulsd	(%rdx), %xmm0, %xmm0  ; xmm0 *= *rdx
    	addq	$8, %rdx    			 ; rdx += 8
    	cmpq	%rax, %rdx				 ; 循环比较
    	vmovsd	%xmm0, (%rbx)		 ; *rbx = xmm0
    	jne		.L22					 ; 循环跳转

    其实就是把 xmm0 当作一个前缀积的变量, 每个位置乘一次赋值一次

现代处理器

Concurrency 与 Parallelism

并行(Parallel): 同一时间内同时执行多条指令, 是物理意义上确实在同时执行的, 常见的例子:

  • 流水线一个周期内同时处理多个指令的不同阶段, 第四章博客已经详细分析过其机制了
  • 多执行单元乱序执行(超标量)
  • 现代多核心 CPU

并发(Concurrency): 通过快速切换任务使得看起来”在同时运行多个任务”, 核心是调度

  • 单核 CPU 上的的多线程(多线程也可能并行实现, 但是单核心 CPU 上就必然是并发的了)
  • 操作系统进程并发(上下文切换)
  • 操作系统中断处理

超标量实现的总体过程: ICU, EU, 退役单元

  • 指令控制单元的 [fetch, 从 I-Cache 种取指令] 和 [decode, 分解为更细化的指令], 如有分支则通过投机执行进行分支预测(也可能有条件传送), 这两个阶段都比第四章设计的 PIPE 处理器的阶段要复杂一些(前者从缓存取指, 后者有指令分解)

  • 执行单元有多个单元进行实际的指令(例如一个 load 单元会有一个加法器进行地址计算), 这些单元会和 D-Cache 取指令

  • 指令控制单元中有退役单元, 一些涉及分支预测/条件传送的代码会很早就被计算出结果(影响), 只有这条指令计算完成并且引起这条指令的分支点也被确认为预测正确, 才会同步到架构寄存器(退役), 否则会被清空并且丢弃;

  • 通过寄存器重命名暂时存储一些中间值, 使得多级分支预测或者更复杂的控制流可以高效执行
    退役单元负责把功能单元计算出的还未确认能够被执行的影响作为一个标记 \((\text{condition, reg, value})\), 如果有某个指令是需求这个 \(\text{condition}\) 下的寄存器 \(\text{reg}\) 值, 就直接用这个标记包含的值 \(\text{value}\), 而不用真的等前面的分支指令都退役了才继续向下(由此看出超前执行了非常多的指令)

  • 这种结构称之为乱序处理, 与流水线一样是现代 CPU 高速处理的必杀武器

功能单元的性能

延迟是这条指令需要执行的周期数, 发射时间 \(I\text{ (clock cycles)}\) 是依赖流水线时最多两条相同指令的间隔(还记得我们第四章说的暂停插入气泡和转发吗?), 容量 \(C\text{ (clock cycles)}\) 是能够执行这一指令的功能单元数量

发射时间为 \(1\) 是完全流水线化的, 最大吞吐量定义为发射时间的倒数用于评估指令在流水线中的性能, 处理器的总吞吐量就是 \(C \times 1/I\) (容量乘以指令最大吞吐量)

更加底层的程序优化

程序的数据流图: (非正式地) 用以表示程序在具体 decode 后的指令级别执行的顺序和依赖关系, 可以归纳出关键路径从而得出 CPE 瓶颈

1
2
3
4
5
6
7
8
9
10
11
/* Accumulate result in local variable */ 
void combine4(vec_ptr v, data_t *dest) {
	long i; 
    long length = vec_length(v); 
    data_t *data = get_vec_start(v); 
    data_t acc = IDENT;
	for (i = 0; i < length; i++) {
		acc = acc OP data[i];
    }
	*dest = acc; 
}
1
2
3
4
5
.L25:
	vmulsd	(%rdx), %xmmO, %xmmO
	addq 	$8, %rdx
	cmpq 	%rax, %rdx
	jne 	.L25
1
2
3
4
5
6
7
8
9
10
11
12
; decode 扩展后的指令
.L25:
    ; vmulsd	(%rdx), %xmmO, %xmmO
    movsd (%rdx), %xmm1            # load <- %rdx
    mulsd %xmm1, %xmmO             # %xmm0 <- mul <- (xmm0, load)
    
    addq $8, %rdx                  # %rdx <- add <- %rdx

    cmpq %rax, %rdx                # cmp <- (%rax, %rdx), 其中 %rax 是 add 后的

    jne .L25                       # jne <- cmp

例如对这个代码, 用到了 %rax, %rdx, %xmm0 三个寄存器, 分别存储 length, data[i] 和 acc

写出汇编并且解码为细化操作后就很容易得出数据流图:

  • %rax -> cmpq -> jne
  • %rdx(1) -> load -> mul
  • %rdx(2) -> add -> cmpq -> %rdx
  • %xmm0 -> mul -> %xmm0
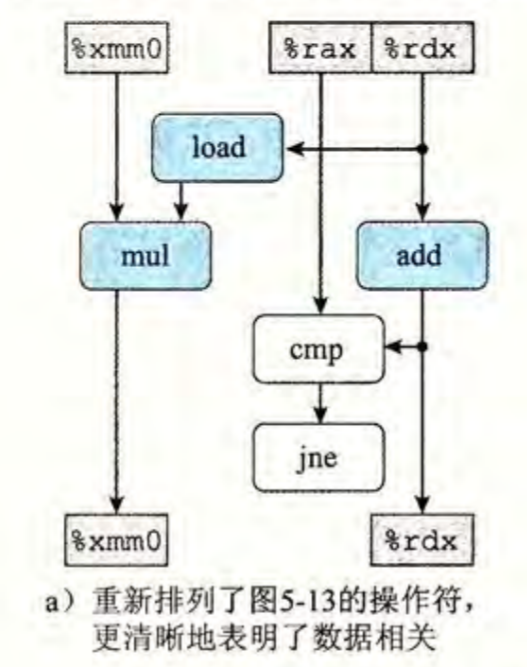
CSAPP3e 图 5-14 a)

这是单次循环的, 把多次循环的数据流图合并起来:

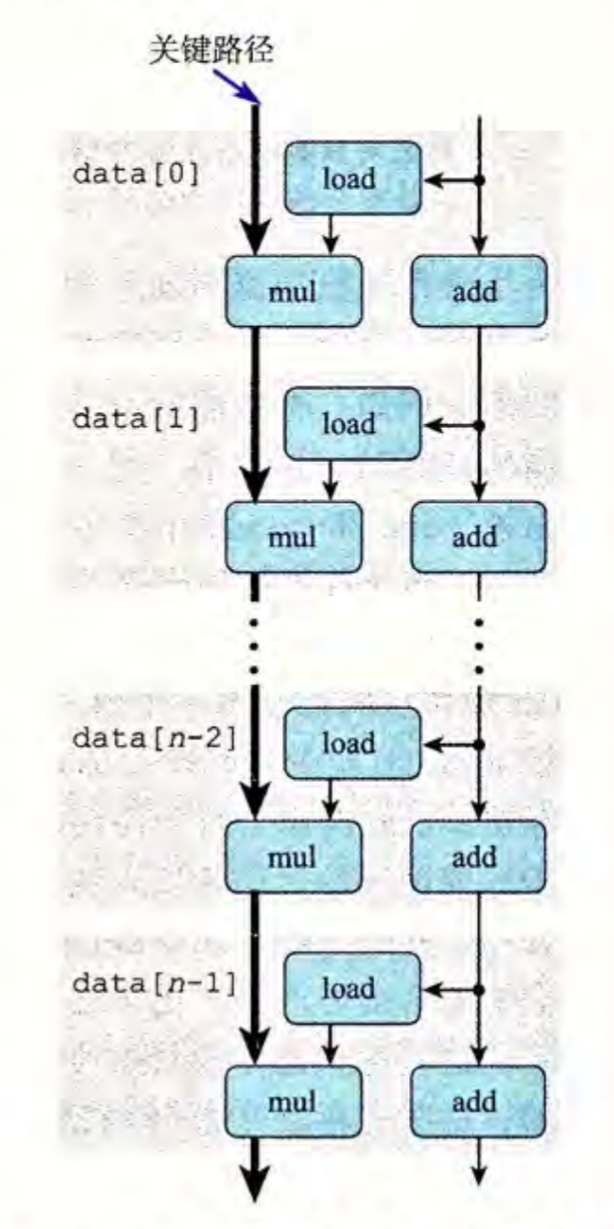
CSAPP3e 图 5-15

发现 %rdx (2) 就是关键路径 (因为浮点乘法延迟 5 周期, 整数加法延迟 1 周期)

各种接近底层的优化:

  1. 减少关键路径 CPE

以 CSAPP 的习题举例子, 计算多项式 \(a_0 + a_1x + a_2x^2 + ... + a_nx^n\) 的两个代码

1
2
3
4
5
6
7
8
9
10
11
// 正常计算
double poly(double a[], double x, long degree) {
	long i; 
    double result = a[0]; 
    double xpwr = x;
    for (i = 1; i <= degree; i++) {
		result += a[i] * xpwr; 
        xpwr = x * xpwr;
    }
	return result;
}

秦九韶算法: \(a_0 + a_1x + a_2x^2 + ... + a_nx^n = a_0 + x(a_1 + x(a_2 + ... + x(a_{n-1} + xa_n)...))\)

1
2
3
4
5
6
7
8
9
// 秦九韶算法 https://en.wikipedia.org/wiki/Horner%27s_method
double polyh(double a[], double x, long degree) {
	long i; 
    double result = a[degree]; 
    for (i = degree-1; i >= 0; i--) {
		result = a[i] + x * result;
    }
    return result;
}

后者的数据依赖太强(必须 x * result 计算完成并且 a[i] 加载完成后才能累加到 result), 关键路径太长: 一个迭代内一个浮点乘法和一个浮点加法是 \(\text{CPE} = 5 + 3 = 8\)

前者的 result 只需要等 a[i] 加载完就可以累加, 而 xpwr 的累乘在另一条路径上, 所以关键路径就单纯是一条浮点乘法 \(\text{CPE} = 5\)

  1. 循环展开

一下是一个循环展开的例子:

1
2
3
4
5
6
7
8
for (int i = 0; i < n; i++) {
    acc += data[i];
}
// 2 x 1 循环展开
for (int i = 0; i < n; i += 2) {
    acc += data[i];
    acc += data[i + 1];
}

循环展开最直观的优化就是减少了循环判断和跳转的操作数量, 通过合适的优化我们也可以减少关键路径上的操作数量。
当然如果你画一下上面这个循环展开的数据流图, 会发现这是不会缩短关键路径的, 要想显著缩短循环路径, 还需要进一步减少数据依赖 提高指令并行性

  1. 提高指令并行性(多个累计变量, 重新结合变换)

    • 多个累计变量

      1
      2
      3
      4
      5
      6
      // 2 x 2 循环展开
      for (int i = 0; i < n; i += 2) {
          acc0 += data[i];
          acc1 += data[i + 1];
      }
      acc = acc0 + acc1;

      刚刚 $ 2 $ 的循环展开没能缩短关键路径的原因是 acc 造成了数据依赖, 必须一个 data[i] 累加完后才能累加下一个 data[i + 1], 这里我们用两个累计变量, 形成两条并行的关键路径, 每条关键路径上就有 \(n / 2\) 个操作

    • 重新结合变换

      1
      2
      3
      4
      5
      6
      7
      8
      9
      // 2 x 1 循环展开
      for (int i = 0; i < n; i += 2) {
          acc += (acc OP data[i]) OP data[i + 1];
      }

      // 2 x 1a 循环展开
      for (int i = 0; i < n; i += 2) {
          acc += acc OP (data[i] OP data[i + 1]);
      }

      乍一看十分令人迷惑, 怎么换个括号的结合就能变快呢?

      原理同样是减少数据依赖. $ 2 $ 循环展开中是必须累乘完 data[i] 才能累乘 data[i + 1], acc 造成了数据依赖, 而 $ 2 1a $ 循环展开中, data 的累乘和 acc 的累加是两条并行的路径, 每条关键路径上有 \(n / 2\) 个操作

来一个小练习, 计算不同结合下的浮点乘法 CPE 下界:

计算不同结合下的浮点乘法 CPE 下界

重新结合的优化是有前提的: 补码任意可结合, 但浮点数可交换不可结合。不过但有些情况特殊, 权衡性能与出错的数据概率。

总结一下各种优化的原理:

  • 循环展开: 减少计算无关指令数量, 减少关键路径操作
  • 多个累计变量: 减少指令间相互的数据依赖
  • 重新结合同样是减少指令间的依赖, 并且最大程度利用处理器的多个同一操作的功能单元

限制因素

  • 过度循环展开会导致寄存器溢出, 在栈上处理数据反而变慢

  • 分支预测错误惩罚, 其实没事, 但要注意一些原则(通过特殊编码风格充分利用条件传送)

    一个利用条件传送的例子(字太乱见谅)

内存操作性能

  • 加载延迟(在 CSAPP 参考机上)是 \(4\) 周期, 但发射 \(1\) 周期, 应当减少数据依赖使得其能够达到完全流水线化
  • 存储同理, 而且存储必须在下一次加载之前, 依赖条件很多, 可以看一下下一章的存储器缓存和空间局部性博客

一个很厉害但是自己完全做不到的实例

程序剖析(profiling)

利用 Unix gprof, 配合 gcc 的 -pg (鼙鼓) 选项获得每个函数的时间和被调用次数(注意这个是靠时钟中断实现的)

想了下这部分书上讲的比较详细了, 我也没什么新的感想, 没有必要复述一遍, 感兴趣的可以回去看书, 其给出的例子从 \(3.5\text{ min}\) 到 \(0.2\text{ s}\) 的优化例子

Amdahl’s Law

可以复习一下之前博客说过的 \(\text{Amdahl}\) 定律 (距离写那篇文章已经四年多过去了, 白驹过隙啊): 我回去看了眼写得还行, 就直接贴过来了:

设一个操作原来需要 \(T_{old}\) 的时间执行, 现在我们对其 \(a\) 的部分(即 \(\text{总部分}\times\text{a}\) 这部分进行\(1/k\)的优化(原来这部分 \(T\) 时间可以执行完, 现在加速到了 \(T/k\) ), 则

  • 没有加速的部分所需时间: \((1-a)\times T_{old}\)
  • 加速的部分所需时间: \((a\times T_{old})/k\)

所以总体加速后的时间为

\[ T_{new}=(1-a)\times T_{old} + (a\times T_{old})/k \]

所以加速比 \(S=T_{old}/T_{new}\) 就是

\[ \begin{aligned} S &= \frac{T_{old}}{T_{new}} \\ &= \frac{T_{old}}{(1-a)\times T_{old} + (a\times T_{old})/k} \\ &= \frac{1}{(1-a)+a/k} \end{aligned} \]

常见的表示方法是用算出的加速比后加上一个”\(\times\)“,我们对 \(60\%\) 的部分进行优化, 这部分执行时间到了原来的 \(1/3\) , 则 \(a=0.6, k=3\) ,带入公式得出 \(S=1.67\) , 则加速比就是 \(1.67 \times\), 读做”1.67倍”.

  • 当 \(k\) 趋向于 \(\infty\) 时, 这部分时间可以忽略不计, 于是就有 \[S_{\infty}=\frac{1}{(1-a)}\] 即使 \(60\%\) 的系统可以加速到可以忽略时间的程度, 总体加速比也只有 \(2.5 \times\), 这体现了Amdahl 定律的一个重要思想:

只有提升了系统的大部分, 才能更好的提升整个系统